WLS#
Use Cases:
Using observed data to represent a larger population: Suppose you are using a sample from a survey that oversampled from some groups. We could use the survey weights in a WLS to minimize SSE with respect to the population instead of the sample. Let \(\pi_g\) be the population share of group g. And let \(h_g\) be the sample share of group G. Then define weight for unit i to be \(w_i\) as \(\frac{pi_{gi}}{h_{gi}}\).
duplicate observations (or aggregated data): if observations with covariates {X_i} appear multiple times, you could include these observations just once and set \(w_i\) to be the number of times they appear.
Unequal variance: if there is a lot of heteroskeasticity, you can set weights to the inverse of the error variance
import numpy as np
import pandas as pd
import statsmodels.api as sm
import seaborn as sns
import patsy
# create two groups for error variance, low and high
n = 300
np.random.seed(0)
df = pd.DataFrame({
"x1":np.random.normal(10,1,n),
"e":np.random.normal(0,1,n)
}).sort_values('x1')
sigma = 0.5
w = np.ones(n)
w = df["x1"] / 2
df["y_true"] = 2 + 3*df["x1"]
df["y_obs"] = df["y_true"] + w*sigma*df["e"]
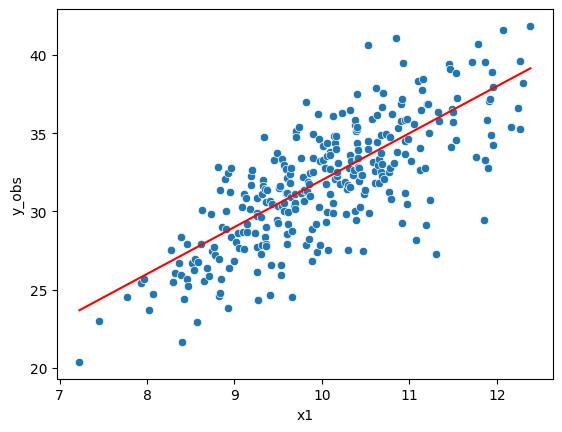
sns.scatterplot(df["x1"], df["y_obs"])
sns.lineplot(df["x1"], df["y_true"], color="red")
/home/chansoo/projects/statsbook/.venv/lib/python3.8/site-packages/seaborn/_decorators.py:36: FutureWarning: Pass the following variables as keyword args: x, y. From version 0.12, the only valid positional argument will be `data`, and passing other arguments without an explicit keyword will result in an error or misinterpretation.
warnings.warn(
/home/chansoo/projects/statsbook/.venv/lib/python3.8/site-packages/seaborn/_decorators.py:36: FutureWarning: Pass the following variables as keyword args: x, y. From version 0.12, the only valid positional argument will be `data`, and passing other arguments without an explicit keyword will result in an error or misinterpretation.
warnings.warn(
<Axes: xlabel='x1', ylabel='y_obs'>
With known weights:#
f = 'y_obs ~ x1'
y, X = patsy.dmatrices(f, df, return_type='dataframe')
mod = sm.WLS(y, X, weights = 1 / (w**2))
res = mod.fit()
print(res.summary())
WLS Regression Results
==============================================================================
Dep. Variable: y_obs R-squared: 0.611
Model: WLS Adj. R-squared: 0.610
Method: Least Squares F-statistic: 468.6
Date: Thu, 01 Jun 2023 Prob (F-statistic): 4.21e-63
Time: 12:46:06 Log-Likelihood: -699.33
No. Observations: 300 AIC: 1403.
Df Residuals: 298 BIC: 1410.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.7195 1.412 0.510 0.611 -2.059 3.498
x1 3.0946 0.143 21.648 0.000 2.813 3.376
==============================================================================
Omnibus: 1.909 Durbin-Watson: 2.015
Prob(Omnibus): 0.385 Jarque-Bera (JB): 1.671
Skew: -0.174 Prob(JB): 0.434
Kurtosis: 3.109 Cond. No. 98.7
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Estimating Weights#
Here, we do not know the weights. To estimate them, we start by running simple OLS to get residuals. Next, we regress root of absolute value of residuals against X and save fitted values. Last, we run a weighted least squares model, using the fitted values as \(\sigma\). Then weights are \(1 / \sigma^2\)
Lots of different methods, see here for more details.
# simple OLS without weights
f = 'y_obs ~ x1'
y, X = patsy.dmatrices(f, df, return_type='dataframe')
mod_ols = sm.OLS(y, X)
res_ols = mod_ols.fit()
# regress root of absolute deviation against X
mod_resid = sm.OLS(np.sqrt(abs(res_ols.resid)), X)
res_resid = mod_resid.fit()
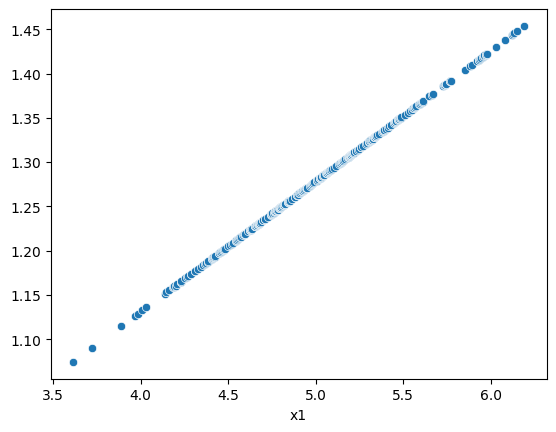
# plot true weights, w against fitted values
sns.scatterplot(w, res_resid.fittedvalues)
/home/chansoo/projects/statsbook/.venv/lib/python3.8/site-packages/seaborn/_decorators.py:36: FutureWarning: Pass the following variables as keyword args: x, y. From version 0.12, the only valid positional argument will be `data`, and passing other arguments without an explicit keyword will result in an error or misinterpretation.
warnings.warn(
<Axes: xlabel='x1'>
mod_2stage = sm.WLS(y, X, 1 / (res_resid.fittedvalues**2))
print(mod_2stage.fit().summary())
WLS Regression Results
==============================================================================
Dep. Variable: y_obs R-squared: 0.599
Model: WLS Adj. R-squared: 0.598
Method: Least Squares F-statistic: 445.0
Date: Thu, 01 Jun 2023 Prob (F-statistic): 4.57e-61
Time: 12:46:06 Log-Likelihood: -700.31
No. Observations: 300 AIC: 1405.
Df Residuals: 298 BIC: 1412.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 1.1803 1.440 0.820 0.413 -1.653 4.014
x1 3.0483 0.145 21.094 0.000 2.764 3.333
==============================================================================
Omnibus: 2.501 Durbin-Watson: 2.027
Prob(Omnibus): 0.286 Jarque-Bera (JB): 2.208
Skew: -0.193 Prob(JB): 0.332
Kurtosis: 3.165 Cond. No. 100.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.